
为了对特定对象进行数值模拟,在CFD中解决的第一步是创建一个函数空间来寻找解。为CFD解决方案构建近似空间意味着将对象分解为更小的单元(与参考的几何形状相关),即生成网格。我们已经提到四边形/六面体网格提供了更好的属性,例如数值稳定性、与物体的物理特征对齐、捕获各向异性、在多结构域上的使用、 更低的计算成本和高效的内存使用。因此,本节阐述一种鲁棒且快速的四边形网格生成法。
四边形网格由以下组成:
• 顶点 V = {vi ∈ R3} 约束每条边,
• 定向边 E = {eij ∈ V × V } 绑定每个单元
• 不同的四边形单元(面/面)F = {fijkl ∈ V4}。
顶点的价是其绑定边的数量,如果顶点具有 4 价,则该顶点是规则的,否则是不规则的。只有一个入射边的边缘被认为是边界; 边界边上的顶点也被认为是边界节点(如图所示)。
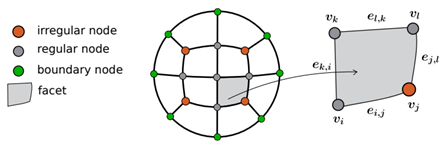
基于其组成部分之间的连通性,四边形网格可以是:
• 协调或非协调
• 结构化或非结构化
如果存在至少两个仅共享边的一部分的面,则四边形网格是非协调的,否则是协调的(任何两个面共享一个顶点,一条完整的公共边),如图所示在下图中,左边为协调网格,右边为非协调网格。

协调网格在工业和科学应用中是首选,因为函数空间的定义很容易,这使得轻量级计算成为可能 ,尽管它们的生成是一项具有挑战性的任务。 非协调网格在文献中通常称为 T 网格,因为一个面的节点位于(另一个面的)边的内部。 可以通过删除/添加节点和边将协调网格转换为非协调网格。 另一方面,反之亦然的过程要么在计算上非常昂贵,要么在算法上难以执行。
结构化和非结构化网格之间的区别主要取决于它们各自连接的性质。 结构化网格连接是隐式的,即元素可以使用 IJK 枚举方案自动存储和访问,而非结构化网格的连接是显式的,即每个元素必须单独描述。 结构化网格的规则连通性与拓扑质量的概念密切相关 ,它还允许根据坐标对相邻元素进行分析查询。在各种模拟中,结构化网格表现出的元素的严格对齐是首选,例如,计算流体动力学中的边界层和结构动力学中的复合材料。
在结构化四边形网格中,可以区分以下三个子类别:全结构化、块结构化和半结构化网格,如下图所示。 全结构化网格是处处结构化的网格,块结构化网格由有限数量的全结构化块组成,而半结构化网格没有获得高层次结构,通常具有大量不规则节点(不被恰好四个四边形包围的节点)。
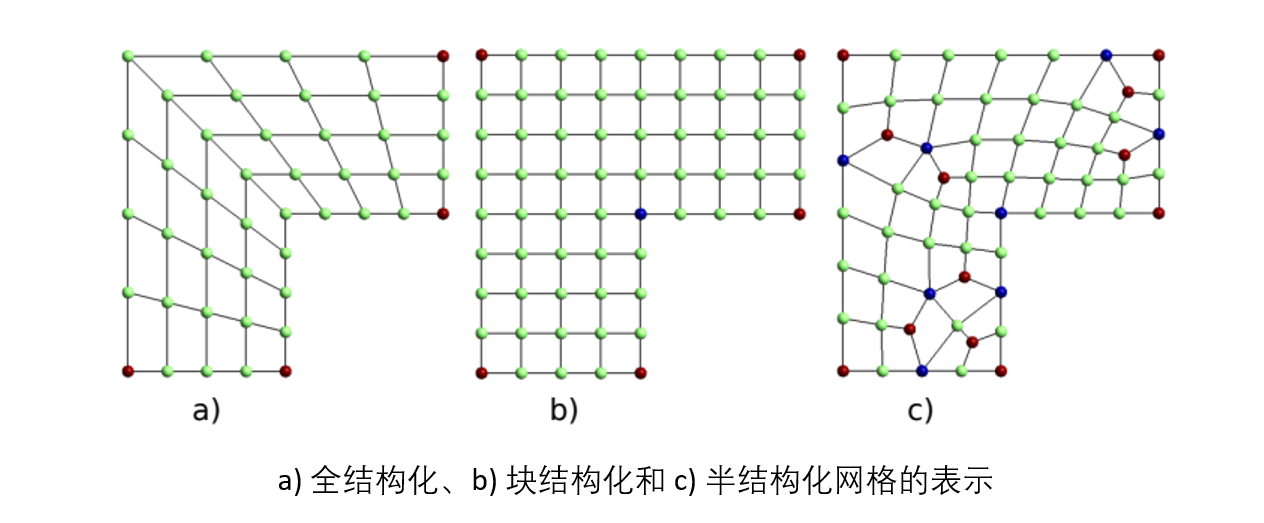
以自动方式在任意表面上创建高质量的四边形网格并非易事。 它意味着满足上述所有属性并遵守表面的拓扑和几何特征。
更具体地说,四边形网格的不规则顶点的数量和价数受欧拉特征 χ 约束,这是表面的拓扑不变量。 为了更好地理解这种拓扑约束,考虑一个“理想的”全结构化网格,其中每个顶点都是规则的,即价数为 4。可以证明只有欧拉特性等于的表面χ = 0 时才是理想的结构化网格,如下 所示为圆环体上的理想四边形网格。通常,结构化网格涉及不规则顶点,即不等于4 价的顶点。
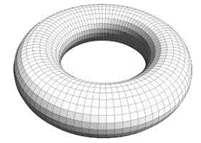
为了说明域的拓扑如何约束不规则节点的数量和价数,我们从欧拉多面体定理开始。 它显示了三维空间 R3 中的可定向曲面 S 的顶点数 V 、边 E 和小平面 F 之间的联系,具有该曲面的欧拉特征 χ(S):
定理:(欧拉多面体定理)
V − E + F = χ(S).
此外,通过利用四边形网格的顶点、边和面的数量之间的关系,可以得出 [4, 5]:
定理:(庞加莱-霍普夫定理)
庞加莱-霍普夫定理定理证明了在 χ ≠ 0 的曲面上出现不规则节点。

上图所示:在不破坏拓扑结构的情况下强加一组 3−5 价不规则节点。 每个立方体面的奇点数最少 a),每个立方体面的奇点数增加 b)。价 = 3 的不规则节点为红色,价 = 5 为蓝色。
值得注意的是,边界点阵中具有价数为5和3的两个顶点在求和中会相互抵消。这表明四边形网格中不规则节点的数量可能会任意增加(参见图7.13),从而影响其可用性。上述的拓扑约束并不是生成适用于CFD 四边形网格的所有复杂性, 另一个限制来自几何——保留对象的特征(边界和曲线形状)或子区域(包括但不限于:重叠的布局、布局区域之间的间隙或交叉点),由此导致四边形网格划分确实是一项非常受限且具有挑战性的任务。
基于块结构化四边形网格的特点,我们使用一组基于计算对象表面多边形布局的方法,该方法旨在划分几何形状以便可以对获得的多边形布局的每个区域进行单独处理,以生成高质量的四边形网格。
多边形布局的结构属性
几何对象的表面多边形布局由以分区边缘(即弧和节点)为界的面片组成。 以两个奇点为界的弧链称为分线,如图 7.14 所示。 一个奇点产生的分线的个数决定了它的价数4。两个分线或一个分线与边界相交得到的节点称为交点。
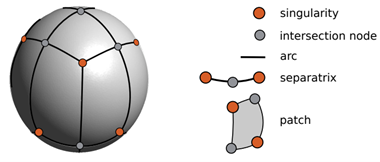
如果存在两个仅共享弧的一部分的补丁,则多边形布局是非协调的,其切割产生 T 形接头。
从多边形布局开始,通过单独重新划分每个面片的网格,可以轻松获得具有控制尺寸和元素各向同性的块结构四边形网格。 实现这一目标的巨大挑战是确保多边形布局具有高质量(如共形、形状良好、与模型的特征对齐)。 过去,这项任务依赖于繁琐的手工作业,而如今,我们正探索依靠具有强大数学背景的合适算法。
通过交叉场自动生成多边形布局
生成表面多边形布局的任务可以通过直接算法、谱方法、参数化方法或方向场跟踪技术来完成。交叉场即四个对称方向场,对于四边形网格的生成是无处不在的,本文特别关注交叉场,多边形布局(和最终的四边形网格)的质量在很多方面与初始的交叉场有关。为了展示这种联系,以下将讨论交叉场的表示、计算和特征。

交叉场作为一种特殊类型的方向场,因其张量性质和引导、缩放与定向四边形网格的能力而备受四边形网格研究者的关注。换句话说,交叉场可以被视为具有无限小的四边形集合,其边缘与交叉场分支对齐。在局部范围内,交叉场特征强制与四边形单元的方向和大小相关。此外,可以证明交叉场具有对应于四面网格不规则顶点位置的孤立奇点,这使得交叉场成为一种流行的辅助对象,可在其上构建高质量的块状四面网格。
从交叉场生成多边形布局,可以使用显式和参数化方法。前者依赖于追踪从交叉场奇点发射的分离线,以划分多边形区域,此时它们的有效性和形状可以得到改善。多边形布局代表了一种用于参数化、获取细分曲面和形状抽象的有效结构。可以以不同的方式将几何域划分为块,并且根据背景场获得的块可以是非结构化的、病态的或高质量的。获得的分区的形状、数量、变形程度和结构等属性极大地影响最终的四边形网格。
获得的最理想的分区特征是布局简单性、结构化、一致性、矩形性以及特征和主方向对齐 [6]。 这种满足这些属性的特定类别的多块网格称为四边形布局。 模型的四边形布局可以生成多块结构化网格,生成纯四边形布局的优点很多,然而,它们确实是需要复杂且耗时的算法,并且代价高昂。
我们更进一步放弃了要求区块布局为一定为四边形的约束,赋予我们更大的灵活性,这在我们的例子中是必要的,可以嵌入任意特征线作为布局边界,这得益于我们在非矩形区域的四边形网格划分方面取得的进展。
之后,几何表面的各个多边形分区通常由核心算法单独重新划分四边形网格,并且这些算法易于实现,计算成本低,并且仅适用于简单的几何图形,或者像本例中的小块—它们在拓扑上满足一些基本条件。
局部区域四边形网格生成
请注意,我们只考虑当前CAD模型的面S中子区域的四边形网格划分,而不考虑模型的全局四边形网格。
当面S中子区域的拓扑结构足够简单时,我们使用一种预定义的拓扑方法对整个面S中的所有子区域进行网格化。对于每种满足条件的简单子区域我们预定义的多种四边形网格拓扑。
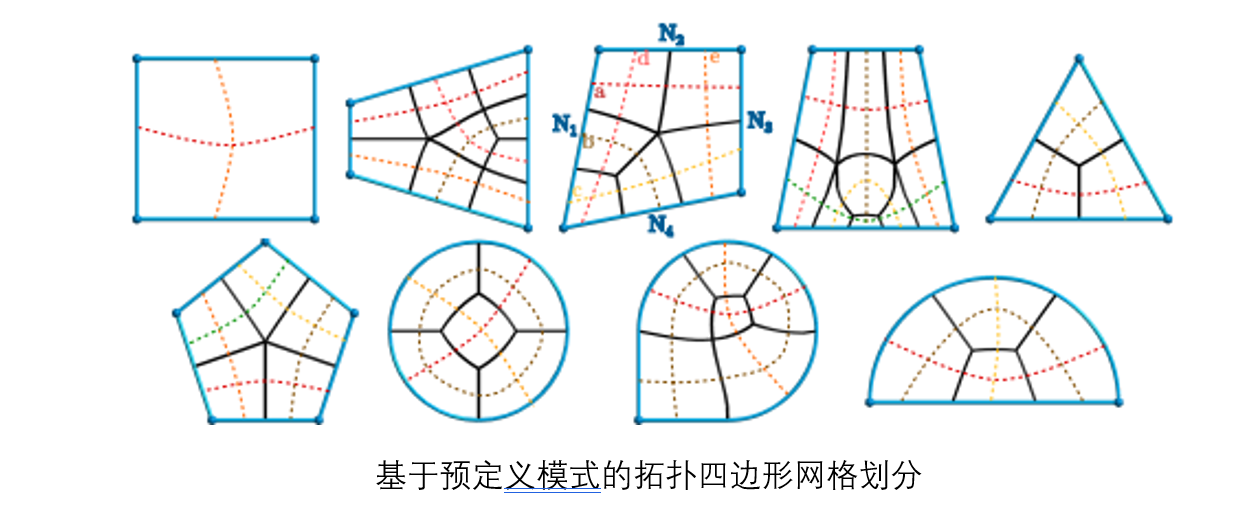
考虑具有m个侧边缘(N1,…,Nm)的子区域面片,首先检查在我们预定义的模式列表中是否能找到具有m个边的匹配模式(例如图7-16)。对于每个模式P,我们将(s1,…,sc)指定为模式的c个拓扑弦的边缘细分数(图7-16中虚线)。如果可以找到严格正的弦细分sj> 0,j∈[1,c],使得在每个边上包含在边中的弦的细分之和等于边的数量,则可以划分高质量四边形网格。

我们可以看到 b 必须遵守 b = N3 − N1 和 b = N4 − N2,如果我们查看对偶和弦(下图所示),这是一个非常自然的条件。 另一方面,如果 N3 − N1 ≠ N4 − N2,则此模式无解。 假设满足上述条件,各个细分 a、c 和 d、e 之间的平衡留给目标函数的最小化解。
面网格数据结构的选择
重拓扑的面网格生成算法的效率和内存消耗很大程度上取决于底层的表面网格数据结构。选择网格数据结构需要同时考虑拓扑和算法方面的考虑:
评估一个数据结构需要度量各种标准,比如需要(a)时间来预处理期间构造它,(b)时间来处理一个特定查询,(c)时间来执行一个特定操作,以及(d)内存消耗和冗余。
基于半边的数据结构(Halfedge-Based Data Structure)
半边数据结构通过将每个(无方向的)边分割成两个有方向的半边,避免了基于边的数据结构的单环遍历区分,如下图所示。 这种数据结构能够表示可定向(组合)2-流形(没有复杂的边和顶点,见图7.17)的子集的任意多边形网格。
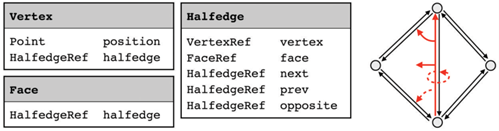
半边数据结构中,半边沿每个面和每个边界以一致的逆时针顺序排列。因此在这里,每个边界都可以被看作是潜在高度的空白面。额外地,每个半边指定了一个唯一的角(面中的一个非共享顶点),因此纹理坐标或法线等属性可以存储在每个角上。
对于每个半边,我们存储对以下对象的引用:
其指向的顶点
其相邻的面(如果是边界半边,则为零指针)
面或边界的下一个半边(逆时针方向)
面的前一个半边
其对(或逆)半边
注意,如果两个对半边总是成对地分组并存储在后面的数组位置halfedges[i]和halfedges[i+1]中,则不需要存储对半边。对半边由加上取模2隐式给出。此外,将两条半边组成一对,我们就得到了一个完整边的表示,这在当我们想要将数据与边关联,而不是与半边关联时是很重要的。而一个面中的前一条半边的引用也可以省略,因为这可以通过步进下一个半边引用得到。
此外,每个面存储它的其中一个半边的引用,每个顶点存储一个外射的半边。由于半边数大约是是顶点数的6倍,总内存消耗是16字节/顶点+20字节/半边+4字节/面=144字节/顶点。不显式地存储前一个和对半边则将内存成本降低到96字节/顶点。
半边数据结构使我们能够枚举每个元素(即顶点,边,半边或面)的所有相邻元素。特别是,现在可以列举给定顶点的单环邻域,而不需要低效的区分,如下图所示。

上图中心顶点的单环邻域可以通过从中心顶点的外射半边开始(左),然后通过步进到对半边(中)和下一个半边(右)顺时针重复旋转,直到再次到达第一个半边枚举得到。
秩益科技有限责任公司 页面版权所有 粤ICP备2023060583号